Matrix Viewer

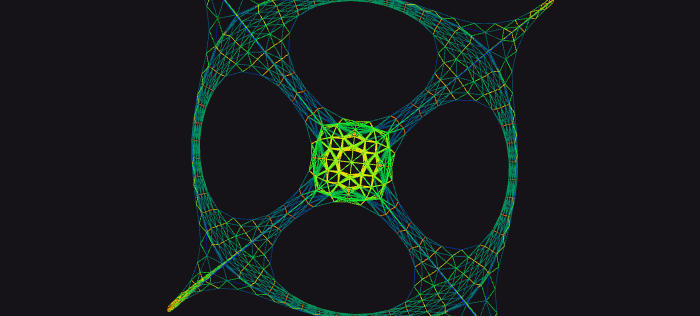
The Web Matrix viewer was made to display pre-calculated graphs of sparse matrices. Sparse matrices are simply big data tables that mostly consist of zeros. Based on work by Tim Davis and Yifan Hu at the University of Florida, I built a program to calculate a somewhat stable shape for a graph representation of sparse matrices. What you see here is the output, visualized in three dimensions.

The basic premise is quite simple: data points are edges in a graph, and each column or row is a node. Then, you have nodes repel one another, and edges draw them closer. Simulate the physics for a bit, and if all goes well you’ll have a stable state. Naturally, in practice it tends to be a bit more difficult. Such simulations can spiral out of control, with forces getting larger and larger. Or simply fail to find a singular stable state. One solution to this is to simply reduce the movement as a function of simulation time, which guarantees you’ll reach a stopping point (as long as it doesn’t shoot off to infinity).

The resulting configuration aims to be a representation of the shape of the matrix. The connectivity of different pieces, and overall structure. Of course, this doesn’t necessarily result in any practical insights. But it often looks interesting, and can provide a valuable visual representation of the data. I find that whatever I’m working with, having a solid visual helps me wrap my head around it. Finally, it’s something you can share with people regardless of their knowledge of your work. “This is the data I’m working with,” and anyone can look at it and say, “Huh, that looks cool.”

On the technical side of things, the visualization was made using Mathbox and javascript. The stable state calculation was made in Unity & C#, though the choice was purely of convenience. It’s not optimized, but it works and you can watch it chug along. The whole process would undoubtedly be a lot quicker without visualizing it in tandem, but that’s part of the fun.

Here are some matrices visualized:

All matrices are from the University of Florida collection.